In the given figure, if PQ = 6, QR = 10, PS = 8 find TS.
Chapter 3 – Circle – Text Book Solution
Practice Set 3.5 | Q 4 | Page 82
In the given figure, if PQ = 6, QR = 10, PS = 8 find TS.
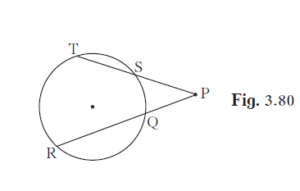
Using the theorem of chords intersecting outside the circle, we have
PT × PS = PR × PQ
⇒ (TS + PS) × PS = (QR + PQ) × PQ
⇒ (TS + 8) × 8 = (10 + 6) × 6
⇒ 8TS + 64 = 16 × 6 = 96
⇒ 8TS = 96 − 64 = 32
⇒ TS = \[\frac{32}{8}\] = 4 units
Explanation:-
To solve the problem, we use the theorem of chords intersecting outside the circle, which states that the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
We have PT and PS as the two segments of one chord, and PR and PQ as the two segments of the other chord. So, we can write:
PT × PS = PR × PQ
Substituting the given values, we get:
(TS + PS) × PS = (QR + PQ) × PQ
(Here, TS and QR are equal as they are tangents drawn from the same point to the circle)
Simplifying the equation, we get:
(TS + 8) × 8 = (10 + 6) × 6
Expanding the brackets and simplifying, we get:
8TS + 64 = 96
Subtracting 64 from both sides, we get:
8TS = 32
Dividing both sides by 8, we get:
TS = 4 units
Therefore, the length of the tangent segment from the point of contact to the point of intersection of the secant is 4 units.
Chapter 3 – Circle – Text Book Solution
Practice set 3.5 | Q 4 | Page 82
Click Here to see All the Textbook solution of Circle
