In the given figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following. (1) ∠ AOB (2)∠ ACB (3) arc AB (4) arc ACB
Chapter 3 – Circle – Text Book Solution
Practice Set 3.4 | Q 1 | Page 73
In the given figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
(1) ∠ AOB (2)∠ ACB
(3) arc AB (4) arc ACB
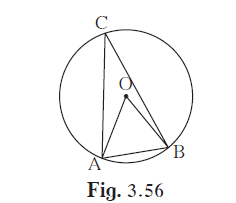
(1) In the given figure, OA and OB are the radii of the circle.
OA = OB = AB (Given)
∴ ∆OAB is an equilateral triangle.
⇒ ∠AOB = ∠OAB = ∠OBA = 60º
Thus, the measure of ∠AOB is 60º.
(2) The measure of an angle subtended by an arc at a point on the circle is half of the measure of the angle subtended by the arc at the centre.
∠ACB = \[\frac{1}{2}\] ∠AOB = \[\frac{1}{2}\] x 60° = 30°
Thus, the measure of ∠ACB is 30º.
(3) m(arc AB) = ∠AOB = 60º (Measure of an arc is the measure of its corresponding central angle)
Thus, the measure of arc AB is 60º.
(4) m(arc ACB) = 360º − m(arc AB) = 360º − 60º = 300º
Thus, the measure of arc ACB is 300º.
Explanation:-
Given: OA = OB = AB
To prove:
- ∠AOB = 60°
- ∠ACB = 30°
- m(arc AB) = 60°
- m(arc ACB) = 300°
Proof:
(1) Since OA = OB = AB, we can conclude that ΔOAB is an equilateral triangle.
Therefore, ∠OAB = ∠OBA = ∠AOB = 60°.
Hence, the measure of ∠AOB is 60°.
(2) According to the theorem, the measure of an angle subtended by an arc at a point on the circle is half of the measure of the angle subtended by the arc at the centre.
So, ∠ACB = ½∠AOB = ½ x 60° = 30°.
Thus, the measure of ∠ACB is 30°.
(3) As we already know that ∠AOB = 60°, using the theorem, the measure of an arc is the measure of its corresponding central angle.
So, m(arc AB) = ∠AOB = 60°.
Thus, the measure of arc AB is 60°.
(4) The sum of the measures of the arcs of a circle is 360°. Therefore,
m(arc ACB) = 360° – m(arc AB) = 360° – 60° = 300°
Thus, the measure of arc ACB is 300°.
Hence, we have proved that ∠AOB = 60°, ∠ACB = 30°, m(arc AB) = 60°, and m(arc ACB) = 300°.
Chapter 3 – Circle – Text Book Solution
Practice set 3.4 | Q 1 | Page 64
Click Here to see All the Textbook solution of Circle
