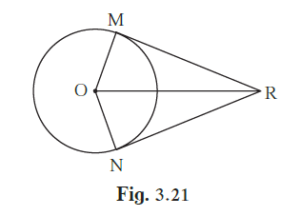
Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON with the help of activity
Chapter 3 – CIrcle- Text Book Solution
Practice Set 3.1 | Q 3 | Page 55
Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON with the help of activity
solution
Proof: In ∆RMO and ∆RNO,
∠RMO ≅ ∠RNO = 90° ......[Tangent theorem]
hypt OR ≅ hypt OR ......[Common side]
seg OM ≅ seg ON ......[Radii of the same circle]
∴ ∆RMO ≅ ∆RNO ......[By Hypotenuse side test]
∠MOR ≅ ∠NOR
Similarly ∠MRO ≅ ∠NRO ......[Corresponding angles of congruent triangles]
Explanation:-
n right triangles RMO and RNO,
- ∠RMO is congruent to ∠RNO and both are 90 degrees (by the Tangent theorem)
- OR is congruent to OR (common side)
- OM is congruent to ON (radii of the same circle) Therefore, by the Hypotenuse-Leg congruence theorem, triangles RMO and RNO are congruent. As a result, ∠MOR is congruent to ∠NOR (corresponding angles of congruent triangles). Similarly, ∠MRO is congruent to ∠NRO.
Chapter 3 – Circle – Text Book Solution
Practice set 3.1 | Q 3 | Page 55
Click Here to see All the Textbook solution of Circle
