1. In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions
Chapter 3 – CIrcle- Text Book Solution
Practice set 3.1
1. In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from
line AB? Why ?
(3) d(A,B)= 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ?
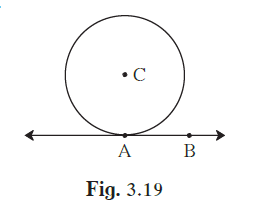
(1) It is given that line AB is tangent to the circle at A.
∴ ∠CAB = 90º (Tangent at any point of a circle is perpendicular to the radius throught the point of contact)
Thus, the measure of ∠CAB is 90º.
2) Distance of point C from AB = 6 cm (Radius of the circle)
/p>((3) ∆ABC is a right triangle.
CA = 6 cm and AB = 6 cm
Using Pythagoras theorem, we have
\[{BC}^2 = {AB}^2 + {CA}^2 \]
\[ \Rightarrow BC = \sqrt{6^2 + 6^2} \]
\[ \Rightarrow BC = 6\sqrt{2} cm\]
Thus, d(B, C) = \[6\sqrt{2}\]
(4) In right ∆ABC, AB = CA = 6 cm
∴ ∠ACB = ∠ABC (Equal sides have equal angles opposite to them)
Also, ∠ACB + ∠ABC = 90º (Using angle sum property of triangle)
∴ 2∠ABC = 90º
⇒ ∠ABC = \[\frac{90^\circ}{2}\]
Thus, the measure of ∠ABC is 45º.
Explanation:-
Line AB is tangent to the circle at point A, which means that angle CAB is a right angle since the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Point C is located 6 cm away from line AB, which is the radius of the circle.
Triangle ABC is a right triangle, with sides CA and AB both measuring 6 cm. By using the Pythagorean theorem, we can calculate the length of side BC as 6√2 cm.
In right triangle ABC, both sides AB and CA are equal in length to 6 cm. Therefore, angles ACB and ABC are also equal, and the sum of these two angles is 90 degrees. This means that angle ABC measures 45 degrees.
Chapter 3 – Circle – Text Book Solution
Practice set 3.1 | Q 1 | Page 55
Click Here to see All the Textbook solution of Circle
