Practice Set 2.2 | Q 3 | Page 43
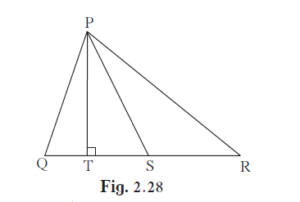
In the given figure, seg PS is the median of ∆PQR and PT ⊥ QR. Prove that,
(i) PR2 = PS2 + QR × ST + `(“QR”/2)^2`
(ii) PQ2 = PS2 – QR × ST + `(“QR”/2)^2`
Answer:- (i) PR2 = PS2 + QR × ST + (QR/2)^2
(ii) PQ2 = PS2 – QR × ST + (QR/2)^2
QS = SR = QR/2 …(1)(S is the midpoint of side QR)
In ΔPTS,
∠T = 90°
According to Pythagoras theorem,
PS2 = PT2 + ST2 …(2)
(i) In ΔPTR, ∠T = 90°
According to Pythagoras theorem,
PR2 = PT2 + RT2
∴ PR2 = PT2 + (ST + SR)2
∴ PR2 = PT2 + (ST + SR)2
∴ PR2 = PT2 + (ST + QR/2)^2
∴ PR2 = PT2 + ST2 + 2ST × (QR/2) + (QR/2)^2 …[(a + b)^2 = a^2 + 2ab + b^2]
∴ PR2 = (PT2 + ST2) + ST × QR + (QR/2)^2
∴ PR2 = PS2 + ST × QR + (QR/2)^2 …[From 2]
(ii) In ΔPTQ, ∠T = 90°
According to Pythagoras theorem,
PQ2 = PT2 + TQ2
∴ PQ2 = PT2 + (QS – ST)2
∴ PQ2 = PT2 + (QR/2 – ST)^2
∴ PQ2 = PT2 + (QR/2)^2 – 2 × QR/2 × ST + ST^2 ..[(a – b)^2 = a^2 – 2ab + b^2]
∴ PQ2 = (PT2 + ST2) – QR × ST + (QR/2)^2
∴ PQ2 = PS^2 – QR × ST + (QR/2)^2 …[From 2]
Chapter 2 – Pythagoras Theorem- Text Book Solution
Practice Set 2.2 | Q 3 | Page 43
