Practice Set 2.1 | Q 9 | Page 39
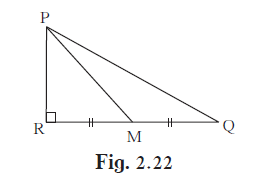
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2
In ∆PRM,
PR2 + RM2 = PM2
⇒ RM2 = PM2 - PR2 ....(1)
In ∆PRQ,
PR2 + RQ2 = PQ2
⇒ PQ2 = PR2 + (RM + MQ)2
⇒ PQ2 = PR2 + (RM + RM)2
⇒ PQ2 = PR2 + (2RM)2
⇒ PQ2 = PR2 + 4RM2
⇒ PQ2 = PR2 + 4(PM2 - PR2) .....(from 1)
⇒ PQ2 = PR2 + 4PM2 - 4PR2
⇒ PQ2 = 4PM2 - 3PR2
Hence, PQ2 = 4PM2 – 3PR2.
Explanation:-
Given that PRM is a triangle. Using the Pythagorean theorem in ∆PRM, we can say that:
PR<sup>2</sup> + RM<sup>2</sup> = PM<sup>2</sup>
Simplifying the equation, we get:
RM<sup>2</sup> = PM<sup>2</sup> – PR<sup>2</sup> ….(1)
Now, consider triangle ∆PRQ. We can apply the Pythagorean theorem in this triangle as well, which gives us:
PR<sup>2</sup> + RQ<sup>2</sup> = PQ<sup>2</sup>
Substituting the value of RQ as (RM + MQ) in the above equation, we get:
PQ<sup>2</sup> = PR<sup>2</sup> + (RM + MQ)<sup>2</sup>
Simplifying further, we get:
PQ<sup>2</sup> = PR<sup>2</sup> + (RM + RM)<sup>2</sup>
PQ<sup>2</sup> = PR<sup>2</sup> + 4RM<sup>2</sup> ……..(2)
Substituting the value of RM<sup>2</sup> from equation (1) in equation (2), we get:
PQ<sup>2</sup> = PR<sup>2</sup> + 4(PM<sup>2</sup> – PR<sup>2</sup>)
Simplifying further, we get:
PQ<sup>2</sup> = PR<sup>2</sup> + 4PM<sup>2</sup> – 4PR<sup>2</sup>
PQ<sup>2</sup> = 4PM<sup>2</sup> – 3PR<sup>2</sup>
Hence, PQ<sup>2</sup> = 4PM<sup>2</sup> – 3PR<sup>2</sup>.
Chapter 2 – Pythagoras Theorem- Text Book Solution
Practice Set 2.1 | Q 9 | Page 39
