In ▢ABCD, seg AD || seg BC. Diagonal AC and diagonal BD intersect each other in point P. Then show that \[\frac{AP}{PD} = \frac{PC}{BP}\]
Problem Set 1 | Q 11 | Page 29
In ▢ABCD, seg AD || seg BC. Diagonal AC and diagonal BD intersect each other in point P. Then show that \[\frac{AP}{PD} = \frac{PC}{BP}\]
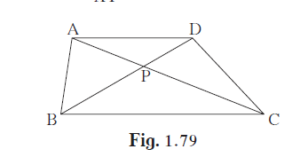
Given: ▢ABCD is a parallelogram
To prove: \[\frac{AP}{PD} = \frac{PC}{BP}\]
Proof: In △APD and △CPB
∠APD = ∠CPB (Vertically opposite angles)
∠PAD = ∠PCB (Alternate angles, AD || BC and BD is a transversal line)
By AA test of similarity
△APD ∼ △CPB
\[\therefore \frac{AP}{PC} = \frac{PD}{PB} \left( \text{ Corresponding sides are proportional } \right)\]
\[ \Rightarrow \frac{AP}{PD} = \frac{PC}{PB}\]
Hence proved.
Answer:_
Given: ▢ABCD is a parallelogram
To prove: [\frac{AP}{PD} = \frac{PC}{BP}]
Proof:
Consider △APD and △CPB.
We have,
- ∠APD = ∠CPB (Vertically opposite angles)
- ∠PAD = ∠PCB (Alternate angles, AD || BC and BD is a transversal line)
By AA test of similarity, we can say that △APD ∼ △CPB.
Therefore, we can conclude that the corresponding sides of these two triangles are proportional, which gives us:
[\frac{AP}{PC} = \frac{PD}{PB}]
Multiplying both sides by PD/PB, we get:
[\frac{AP}{PD} = \frac{PC}{PB}]
Hence, the proof is complete.
Problem Set 1 | Q 11 | Page 29
Click Here for All Textbook Soutions of Chapter 1: Similarity
