In ∆ABC, B - D - C and BD = 7, BC = 20 then Find following ratio.
Problem Set 1 | Q 2.2 | Page 27
In ∆ABC, B – D – C and BD = 7, BC = 20 then Find following ratio.
\[\frac{A\left( ∆ ADC \right)}{A\left( ∆ ABC \right)}\]
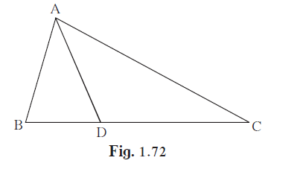
\[\frac{A\left( ∆ ADC \right)}{A\left( ∆ ABC \right)} = \frac{\frac{1}{2} \times AX \times DC}{\frac{1}{2} \times AX \times BC}\]
\[ = \frac{DC}{BC}\]
\[ = \frac{13}{20} \left( \because DC = BC - BD \right)\]
Answer:_
Step 1: Use the formula for the area of a triangle
This step involves applying the formula for the area of a triangle to find the ratio of the areas of ∆ADC and ∆ABC. The formula states that the area of a triangle is equal to half the product of its base and height. We can write this as:
A(∆ADC) = (1/2 * AX * DC) A(∆ABC) = (1/2 * AX * BC)
Step 2: Substitute the expressions for the areas
This step substitutes the expressions for the areas of the triangles from Step 1 into the expression for the ratio of the areas. This gives us:
A(∆ADC)/A(∆ABC) = [(1/2 * AX * DC)/(1/2 * AX * BC)]
Step 3: Simplify the expression
This step simplifies the expression obtained in Step 2 by cancelling the common factor of (1/2 * AX) from both the numerator and denominator. This gives us:
A(∆ADC)/A(∆ABC) = DC/BC
Step 4: Substitute the given values
This step substitutes the given values for DC and BC into the expression obtained in Step 3, which gives us the ratio of the areas of the triangles ∆ADC and ∆ABC as:
A(∆ADC)/A(∆ABC) = 13/20 (since DC = BC – BD)
Problem Set 1 | Q 2.2 | Page 27
Click Here for All Textbook Soutions of Chapter 1: Similarity
