As shown in figure, two poles of height 8 m and........
Practice Set 1.3 | Q 3 | Page 21
As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?
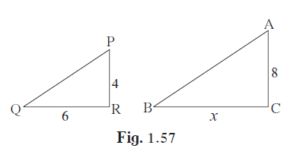
PR and AC are two poles. QR and BC are their shadows respectively."), ("PR = 4, RL = 6, AC = 8"):} ....{"Given"`
∵ The shadows are cast at the same time.
In ΔPQR and ΔABC,
∠PRQ = ∠ACB ...(Each 90°)
∠QPR = ∠BAC ...(Angles made by sunlight on top are congruent)
△PLR ∼ △ABC ...(AA test of similarity)
∵ The shadows are cast at the same time.
In ΔPQR and ΔABC,
∠PRQ = ∠ACB ...(Each 90°)
∠QPR = ∠BAC ...(Angles made by sunlight on top are congruent)
△PLR ∼ △ABC ...(AA test of similarity)
∴ `"PR"/"AC" = "QR"/"BC"` ...(Correspondig sides of similar triangles are in proportion)
∴ `4/8 = 6/x`
∴ `x = (8 × 6)/4`
∴ x = 12
∴ BC = 12m
The length of the shadow of the bigger pole is 12 m.
Answer:-
Given: Two poles of heights 8 m and 4 m respectively are perpendicular to the ground. The length of the shadow of the smaller pole due to sunlight is 6 m.
Since the shadows are cast at the same time, we can use the property of similar triangles to find the length of the shadow of the bigger pole.
Let PR and AC be the two poles, and let QR and BC be their shadows respectively. We have PR = 4, AC = 8, and RL = 6.
In ΔPQR and ΔABC,
- ∠PRQ = ∠ACB = 90° (each 90°)
- ∠QPR = ∠BAC (angles made by sunlight on top are congruent)
Therefore, by AA test of similarity, we have △PLR ∼ △ABC.
Hence, corresponding sides of similar triangles are in proportion i.e., “PR”/”AC” = “QR”/”BC”. We can substitute the given values to find the length of the shadow of the bigger pole.
So, we have 4/8 = 6/x, where x is the length of the shadow of the bigger pole.
Solving for x, we get x = (8 × 6)/4 = 12.
Therefore, the length of the shadow of the bigger pole is 12 m.
Chapter 1. Similarity- Practice Set 1.3 – Page 21
Click Here for All Textbook Soutions of Chapter 1: Similarity
