Chapter 1 Gravitation Text Book Solution Maharashtra Board

Spread the love

Chapter 1 Gravitation Text Book Solution Maharashtra Board

Que 2 :_. What is the difference between mass and weight of an object. Will the mass and weight of an object on the earth be same as their values on Mars? Why?

Answer:- Mass is a measure of the amount of matter in an object, typically measured in units of grams or kilograms. Weight, on the other hand, is a measure of the force exerted on an object due to gravity, typically measured in units of newtons or pounds. The weight of an object is equal to its mass multiplied by the acceleration due to gravity. In everyday use, the terms “mass” and “weight” are often used interchangeably, but in scientific contexts, they have distinct meanings.

The mass of an object will remain the same on Earth as it would on Mars, as mass is a measure of the amount of matter in an object, which does not change. However, the weight of an object will be different on Earth and Mars, as weight is a measure of the force exerted on an object due to gravity, and the acceleration due to gravity is different on the two planets. On Earth, the acceleration due to gravity is approximately 9.8 m/s², while on Mars, it is approximately 3.7 m/s². Therefore, an object with a mass of 1 kg weighs approximately 9.8 N on Earth, but would weigh only 3.7 N on Mars. Chapter 1 Gravitation Text Book Solution Maharashtra Board

b What are (i) free fall

Answer:_

Free Fall :_ Freefall is the motion of an object under the influence of gravity alone, without any propulsion or drag forces acting upon it. It is the motion of an object as it falls to the ground, typically from a height, such as when an object is dropped or when an object falls from the sky. In a state of freefall, an object will accelerate towards the ground at a rate of 9.8 m/s² (on the Earth surface), due to the force of gravity. This acceleration is commonly known as “g-force” or “gravitational acceleration”.

Freefall can be experienced by skydivers, astronauts during spacewalks, and objects dropped from an aircraft or a tower. Some of the freefall motion can be described by the equations of motion such as motion under constant acceleration and motion under the influence of gravity.

ii) acceleration due to gravity :- The acceleration due to gravity, often denoted as “g,” is the acceleration experienced by an object in freefall. The acceleration due to gravity on the Earth’s surface is approximately 9.8 m/s^2, or 1 g. This means that any object in freefall on the Earth’s surface will experience an acceleration of 9.8 m/s² towards the center of the Earth.

In general, the acceleration due to gravity can be calculated using the formula: g = GM / R², where G is the gravitational constant, M is the mass of the celestial body, and R is the distance between the object and the center of the celestial body.

iii) Escape Velocity :_ Escape velocity is the minimum speed required for an object to overcome the gravitational pull of a celestial body and escape into space. It is the speed at which the object’s kinetic energy plus its gravitational potential energy is equal to zero.

For an object to achieve escape velocity, it must be launched vertically upwards with enough initial velocity to overcome the gravitational pull of the celestial body it is trying to escape from. Once an object reaches escape velocity, it will continue to move away from the celestial body at a constant speed, as there is no longer any force acting upon it.

The escape velocity of Earth is about 11.2 km/s or about 25,020 mph.

iv) centripetal force :_ Centripetal force is the force that is responsible for keeping an object moving in a circular path. It is a force that acts on an object in a circular motion and is directed towards the center of the circle. The centripetal force is what keeps an object moving in a circular path, rather than moving in a straight line.

Examples of centripetal force can be found in everyday life, such as the force exerted on a rider of a roller coaster or the force that keeps a car moving in a circular path when it is rounding a bend

c. Write the three laws given by Kepler. How did they help Newton to arrive at the inverse square law of gravity?

Kepler’s first law :

The orbit of a planet is an ellipse with the Sun at one of the foci.

Figure shows the elliptical orbit of a planet revolving around the sun. The position of the Sun is indicated by S.

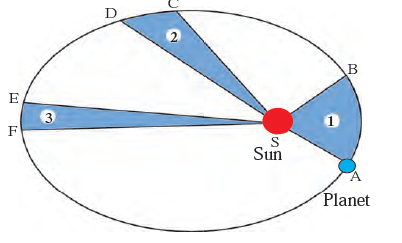
The orbit of a planet moving around the Sun.

Kepler’s second law :

The line joining the planet and the Sun sweeps equal areas in equal intervals of time. AB and CD are distances covered by the planet in equal time i.e. after equal intervals of time, the positions of the planet starting from A and C are shown by B and D respectively.

Kepler’s third law :

The square of its period of revolution around the Sun is directly proportional to the cube of the mean distance of a planet from the Sun.

Newton used Kepler’s third law of planetary motion to arrive at the inverse-square rule. He assumed that the orbits of the planets around the Sun are circular, and not elliptical, and so derived the inverse-square rule for gravitational force using the formula for centripetal force. This is given as:
F = mv²/ r…(i) where, m is the mass of the particle, r is the radius of the circular path of the particle and v is the velocity of the particle. Newton used this formula to determine the force acting on a planet revolving around the Sun. Since the mass m of a planet is constant, equation (i) can be written as:
F ∝ v²/ r…(ii)
Now, if the planet takes time T to complete one revolution around the Sun, then its velocity v is given as:
v = 2πr/ T…(iii) where r is the radius of the circular orbit of the planet
or, v ∝ r/ T …(iv) [as the factor 2π is a constant]
On squaring both sides of this equation, we get:
v² ∝ r²/ T²…(v)
On multiplying and dividing the right-hand side of this relation by r, we get:

v² = 1 \ r² …(vi)
According to Kepler’s third law of planetary motion, the factor r³/ T² is a constant. Hence, equation (vi) becomes:
v² ∝ 1/ r…(vii)
On using equation (vii) in equation (ii), we get:

F = 1/r²
Hence, the gravitational force between the sun and a planet is inversely proportional to the square of the distance between them.

Que:_ A stone thrown vertically upwards with initial velocity u reaches a height ‘h’ before coming down. Show that the time taken to go up is same as the time taken to come down.

Answer : Given; Initial velocity = u; Distance travelled(s) = h; Diagram below shows the situation given in the question;

Time to go up (t1): By Newton’s first equation of the motion

v = u + at

Where v = final velocity; u = initial velocity a = acceleration; t = time taken; A

ccording to our question;

v = 0 (because object has reach a maximum height ‘h’ before coming down and velocity at maximum height is zero);

u= u;

a = -g (because when object will be going up the acceleration due to gravity will be acting downwards to make object to fall. Hence by sign convention direction of motion and acceleration is opposite therefore a is negative);

T = t1;

Putting the values in the equation of motion

we get;

and s = ut + 1/2 at²

∴ s = (v – at)t + 1/2at^{2 + 1/2at²}

s = ut – 1/2 at²

As the stone moves upward from A → B

S = AB = h, t = t₁, a = – g (retardation)

u = u and v = 0

h = 0 – 1/2 (- g)t1²

h = 1/2gt1²

As the stone moves downward from B → A

t = t₂, u = 0, s = h and a = g

h = 1/2gt2²

t1^{2 = t2²}

t1 = t2

e. If the value of g suddenly becomes twice its value, it will become two times more difficult to pull a heavy object along the floor. Why?

Answer : For lifting anybody of mass ‘m’ the force(F₁) required is equal to ‘mg’

where g = acceleration due to gravity;

(Since Force= Mass × Accleration

Therefore F₁ = mg

Now if the value of ‘g’ suddenly becomes twice its value than force(F2) required will be

F₂= m₂g = 2mg

we can see that

F₁/F₂ = 2

Therefore it becomes difficult to pull a heavy object if value of ‘g’ becomes twice its value as double the force is required to overcome the acceleration produced by the force of attraction of earth acting in downward direction

3. Explain why the value of g is zero at the centre of the earth.

Answer : The value of ‘g’ changes as we go inside the earth. According to formula of g = GM/R²

As we go deep inside the earth the Value of ’R’ decreases therefore according to formula the value of ‘g’ should increase. But it is not so because as we go inside the earth towards its center the part of the earth(M) responsible for the gravitational force also decreases that is the value of the ‘M’ also decreases. And due to the combined result of decrease of ‘R’ and ‘M’ the value of ‘g’ decreases as we go inside the earth and is zero at the center of the earth.

4. Let the period of revolution of a planet at a distance R from a star be T. Prove that if it was at a distance of 2R from the star, its period of revolution will be 8 T.

From Kepler’s third law of planetary motion, we have

\[T^2 \propto r^3\] ……….(i)

Thus, when the period of revolution of the planet at a distance R from a star is T, then from

(i), we have

\[T^2 \propto R^3\] …………..(ii)

Now, when the distance of the planet from the star is 2R, then its period of revolution becomes

\[T_1^2 \propto (2R )^3 \]
or
\[ T_1^2 \propto 8 R^3 . . . . . \](iii)

Dividing (iii) by (ii), we get

\[\frac{T_1^2}{T^2} = \frac{8 R^3}{R^3}\]
\[ \Rightarrow T_1 = \sqrt{8}T\]

5. Solve the following examples.

Given: Time (t) = 5 s, height (s) = 5 m

To find: Gravitational acceleration (g)

Formula: s = ut + `1/2 “gt”^2`

Calculation: From formula,

5 = `0 xx 5 + 1/2 “g”(5)^2`

∴ `5 = 1/2 “g” xx 25`

∴ g = `2/5`

∴ g = 0.4 m/s²

The gravitational acceleration of the planet is 0.4 m/s².

b. The radius of planet A is half the radius of planet B. If the mass of A is MA, what must be the mass of B so that the value of g on B is half that of its value on A?

Ans: 2 MA

Solution 1

The acceleration due to gravity of a planet is given as

\[\text{g} = \frac{\text{GM}}{\text{r}^2}\]

For planet A:

\[\text{g}_\text{A} = \frac{\text{GM}_A}{\text{r}_\text{A}^2}\]

For planet B:

\[\text{g}_{B} = \frac{\text{GM}_\text{B}}{\text{r}_\text{B}^2}\]

Now,

\[\text{g}_\text{B} = \frac{1}{2} \text{g}_\text{A}\] …(Given) or,

\[\frac{\text{GM}_\text{B}}{\text{r}_\text{B}^2} = \frac{\text{G M}_\text{A}}{2 \text{r}_\text{A}^2}\]

\[\Rightarrow \text{M}_\text{B} = \frac{\text{M}_\text{A} \text{r}_\text{B}^2}{2 \text{r}_\text{A}^2}\]

Given:

\[\text{r}_\text{A} = \frac{1}{2} \text{r}_\text{B}\]

\[\Rightarrow \text{M}_\text{B} = \frac{\text{M}_\text{A} \text{r}_\text{B}^2}{2(\frac{1}{2} \text{r}_\text{B})^2} = 2 \text{M}_\text{A}\]

Thus, the mass of planet B should be twice that of planet A.

c. The mass and weight of an object on earth are 5 kg and 49 N respectively. What will be their values on the moon? Assume that the acceleration due to gravity on the moon is 1/6th of that on the earth.

Ans: 5 kg and 8.17 N

Given: Mass on earth (me) = 5 kg, weight on earth (W_e) = 49 N,

acceleration due to gravity on moon (g_m) = `9.8/6` m/s² = 1.63 m/s²

To find: Mass (m_m), weight (W_m) on moon

Formula: W_m = m_mg_m

Calculation: The mass of the object is independent of gravity and remains unchanged i.e., 5 kg.

From formula,

W_m = 5 × 1.63

∴ W_m = 8.15 N

On moon, the mass of the object is 5 kg and the weight is 8.15 N.

d. An object thrown vertically upwards reaches a height of 500 m. What was its initial velocity? How long will the object take to come back to the earth? Assume g = 10 m/s2

Ans: 100 m/s and 20 s

Answer :_

From newton’s third equation of the motion;

V² = u² + 2as

Where;

V = Final velocity;

U = initial velocity;

T = time taken;

S = distance travelled;

A = acceleration;

According to our question;

The figure below illustrates the situation given in the question

V = 0 (Velocity at maximum height is zero);

S = 500m ;

A = -10 m/s² (because when object will be going up the acceleration due to gravity will be acting downwards to make object to fall. Hence by sign convention direction of motion and acceleration is opposite therefore a is negative);
Putting the above values we get

0² = u² + (2 x (-10) x 500)

0 = u² – 10000

u² = 10000

⇒ u = √10000 =100

Therefore initial velocity is 100m/s.

From the Newton’s first law of motion;
v = u + at

Where symbols have there usual meanings as above;

v = 0 (velocity at maximum height is zero);

u = initial velocity = 100m/s;

a = – 10m/s² (because when object will be going up the acceleration due to gravity will be acting downwards to make object to fall. Hence by sign convention direction of motion and acceleration is opposite therefore a is negative);
Putting the values we get;

0 = 100 + ( -10t )

= 100 = 10t

t = `100/10` = 10s

Now we know that time required by an object to go up is same as time required to come down.
Therefore;

Total time = time of ascent + time of descent

= 10 + 10 = 20 s

Hence total time to come back to earth is 20 seconds.

e. A ball falls off a table and reaches the ground in 1 s. Assuming g = 10 m/s2, calculate its speed on reaching the ground and the height of the table.

Ans. 10 m/s and 5 m

Solution

g = 10 m/s²

u = 0

Let v be the velocity of the ball on reaching the ground.

Thus, from first equation of motion, we have

v = u + gt

⇒ v = 10 x 1 = 10 m/s

Hence, the speed of the object on reaching the ground is 10 m/s.

Let h be the height of the table. Thus, from the second equation of motion, we have

`”S” = “ut” + 1/2 “gt”^2`

`⇒ “h” = 0 + 1/2 xx 10xx1^2`

⇒ h = 5 m

Hence, the height of the table is 5 m.

f. The masses of the earth and moon are 6 x 1024 kg and 7.4×1022 kg, respectively. The distance between them is 3.84 x 105 km. Calculate the gravitational force of attraction between the two?

Use G = 6.7 x 10-11 N m2 kg-2

Ans: 2 x 1020 N

Solution

the mass of the earth, M = 6 × 10²⁴ kg

the mass of the moon,

m = 7.4 × 10²²

the distance between the earth and the moon,

d = 3.84 × 10⁵ km

= 3.84 × 10⁵ × 1000 m

= 3.84 × 10⁸ m

G = 6.7 × 10^-11 Nm²kg^-2

the force exerted by the earth on the moon is

F = `(“G” “M” xx “m”)/”d”^2`

`= (6.7 xx 10^-11 “Nm”^2″kg”^-2 xx 6 xx 10^24 “kg” xx 7.4 xx 10^22 “kg”)/(3.84 xx 10^8 “m”)^2`

`= ((6.7 xx 10^-11) xx (6 xx 10^24) xx (7.4 xx 10^22))/(3.84 xx 10^8)^2`

`= (6.7 xx 6 xx 7.4)/(3.84 xx 3.84) xx 10^19`

= 2 × 10²⁰N.

Thus the force exerted by the earth on the moon is 2 × 10²⁰N.

Solution

Given: Mass of the earth (M_e) = 6 × 10²⁴ kg,

Gravitational force (F) = 3.5 × 10²² N,

Distance (R) = 1.5 × 10¹¹ m,

Gravitational constant (G) = 6.7 × 10^-11 Nm²/kg²

The gravitational force between the Sun and the Earth can be found out using the formula,

\[F = \frac{GM_e M_s}{R^2}\]

where, Me and Ms are the masses of the Earth and the Sun, respectively. Using all the given values, we have

\[3 . 5 \times {10}^{22} = (6 . 7 \times {10}^{- 11} )\frac{(6 \times {10}^{24} ) \times M_s}{(1 . 5 \times {10}^{11} )^2}\]

\[ \Rightarrow M_s = \frac{(3 . 5 \times {10}^{22} ) \times (1 . 5 \times {10}^{11} )^2}{(6 . 7 \times {10}^{- 11} ) \times (6 \times {10}^{24} )}\]

`= (7.88 \times{10}^{44})/(40.2 xx 10^13)`

= 1.96 × 10³⁰ kg

The mass of the Sun is 1.96 × 10³⁰ kg.